|
|
Partie 3 Les Tests « Il est assez difficile de trouver une erreur
dans son code quand on la cherche. C’est encore bien plus dur quand on est
convaincu que le code est juste. » - Steve McConnell
« Il n’existe pas, et il n’existera jamais, de langage dans lequel il soit un tant soit peu difficile
d’écrire de mauvais programmes ». - Anonyme
« Si le déboguage est l’art d’enlever les bogues, alors la programmation doit être l’art de les
créer. » - Anonyme
Je vous avais dit que l’algorithmique, c’est la combinaison de quatre structures élémentaires.
Nous en avons déjà vu deux, voici la troisième. Autrement dit, on a quasiment fini le programme.
Mais non, je rigole.
Reprenons le cas de notre « programmation algorithmique du touriste égaré ». Normalement,
l’algorithme ressemblera à quelque chose comme : « Allez tout droit jusqu’au
prochain carrefour, puis prenez à droite et ensuite la deuxième à gauche, et
vous y êtes ».
Mais en cas de doute légitime de votre part, cela pourrait devenir : « Allez tout droit
jusqu’au prochain carrefour et là regardez à droite. Si la rue est autorisée
à la circulation, alors prenez la et ensuite c’est la deuxième à gauche.
Mais si en revanche elle est en sens interdit, alors continuez jusqu’à la
prochaine à droite, prenez celle-là, et ensuite la première à droite ».
Ce deuxième algorithme a ceci de supérieur au premier qu’il prévoit, en fonction d’une
situation pouvant se présenter de deux façons différentes, deux façons
différentes d’agir. Cela suppose que l’interlocuteur (le touriste) sache
analyser la condition que nous avons fixée à son comportement (« la rue
est-elle en sens interdit ? ») pour effectuer la série d’actions
correspondante.
Eh bien, croyez le ou non, mais les ordinateurs possèdent cette aptitude, sans laquelle
d’ailleurs nous aurions bien du mal à les programmer. Nous allons donc
pouvoir parler à notre ordinateur comme à notre touriste, et lui donner des
séries d’instructions à effectuer selon que la situation se présente d’une
manière ou d’une autre. Cette structure logique répond au doux nom de
test. Toutefois, ceux qui tiennent
absolument à briller en société parleront également de
structure alternative.
Il n’y a que deux formes possibles pour un test ; la première est la plus simple,
la seconde la plus complexe.
Si booléen Alors
Instructions Finsi
Si booléen Alors
Instructions 1 Sinon Instructions 2 Finsi
Ceci appelle quelques explications.
Un booléen est une expression dont la valeur est VRAI ou
FAUX. Cela peut donc être (il n’y a que deux possibilités) :
Nous reviendrons dans quelques instants sur ce qu’est une condition en informatique.
Toujours est-il que la structure d’un test est relativement claire. Dans la
forme la plus simple, arrivé à la première
ligne (Si… Alors) la machine examine la valeur du booléen. Si ce booléen a
pour valeur VRAI, elle exécute la série d’instructions. Cette série
d’instructions peut être très brève comme très longue, cela n’a aucune
importance. En revanche, dans le cas où le booléen est faux, l'ordinateur
saute directement aux instructions situées après le FinSi.
Dans le cas de la structure complète, c'est à peine plus compliqué. Dans le
cas où le booléen est VRAI, et après avoir exécuté la série d'instructions
1, au moment où elle arrive
au mot « Sinon », la machine saute directement à la première instruction
située après le « Finsi ». De même, au cas où le booléen a comme valeur
« Faux », la machine saute directement à la première ligne située après le
« Sinon » et exécute l’ensemble des « instructions 2 ».
Dans tous les cas, les instructions situées juste après le FinSi seront
exécutées normalement.
En fait, la forme simplifiée correspond au cas où l’une des deux
« branches » du Si est vide. Dès lors, plutôt qu’écrire « sinon ne rien
faire du tout », il est plus simple de ne rien écrire. Et laisser un Si...
complet, avec une des deux branches vides, est considéré comme une très
grosse maladresse pour un programmeur, même si cela ne constitue pas à
proprement parler une faute.
Exprimé sous forme de pseudo-code, la programmation de notre touriste de tout à l’heure
donnerait donc quelque chose du genre :
Allez tout droit jusqu’au prochain carrefour
Si la rue à droite est autorisée à la circulation Alors
Tournez à droite Avancez Prenez la deuxième à gauche Sinon Continuez jusqu’à la prochaine rue à droite Prenez cette rue Prenez la première à droite Finsi
Une condition est une comparaison
Cette définition est essentielle ! Elle signifie qu’une condition est composée de trois éléments :
Les valeurs peuvent être a priori de n’importe quel type (numériques, caractères…). Mais
si l’on veut que la comparaison ait un sens, il faut que les deux valeurs de
la comparaison soient du même type !
Les opérateurs de comparaison sont :
L’ensemble des trois éléments composant la condition constitue donc, si l’on veut, une
affirmation, qui à un moment donné est VRAIE ou FAUSSE.
À noter que ces opérateurs de comparaison peuvent tout à fait s’employer avec des
caractères. Ceux-ci sont codés par la machine dans l’ordre alphabétique
(rappelez vous le code ASCII vu dans le préambule), les majuscules étant
systématiquement placées avant les minuscules. Ainsi on a :
“t” < “w” VRAI
“Maman” > “Papa“ FAUX “maman” > “Papa” VRAI
Remarque très importante
En formulant une condition dans un algorithme, il faut se méfier comme de la
peste de certains raccourcis du langage courant, ou de certaines notations
valides en mathématiques, mais qui mènent à des non-sens informatiques.
Prenons par exemple la phrase « Toto est compris entre 5 et 8 ». On peut
être tenté de la traduire par : 5 < Toto < 8
Or, une telle expression, qui a du sens en français, comme en mathématiques, ne veut rien dire en programmation. En effet, elle comprend deux opérateurs de comparaison, soit un de trop, et trois valeurs, soit là aussi une de trop. On va voir dans un instant comment traduire convenablement une telle condition.
Certains problèmes exigent parfois de formuler des conditions qui ne peuvent pas être
exprimées sous la forme simple exposée ci-dessus. Reprenons le cas « Toto
est inclus entre 5 et 8 ». En fait cette phrase cache non une, mais
deux conditions. Car elle revient à dire
que « Toto est supérieur à 5 et Toto est inférieur à 8 ». Il y a donc bien
là deux conditions, reliées par ce qu’on appelle un
opérateur logique, le mot ET.
Comme on l’a évoqué plus haut, l’informatique met à notre disposition quatre opérateurs
logiques : ET, OU, NON, et XOR.
On représente fréquemment tout ceci dans des tables de vérité
(C1 et C2 représentent deux conditions, et on envisage à chaque fois les quatre cas possibles)
LE GAG DE LA JOURNÉE...
...Consiste à formuler dans un test une condition qui ne pourra jamais être vraie, ou jamais être fausse. Si ce n’est pas fait exprès, c’est assez rigolo. Si c’est fait exprès, c’est encore plus drôle, car une condition dont on sait d’avance qu’elle sera toujours fausse n’est pas une condition. Dans tous les cas, cela veut dire qu’on a écrit un test qui n’en est pas un, et qui fonctionne comme s’il n’y en avait pas. Cela peut être par exemple : Si Toto < 10 ET Toto > 15 Alors… (il est très difficile de trouver un nombre qui soit à la fois inférieur à 10 et supérieur à 15 !) Bon, ça, c’est un motif immédiat pour payer une tournée générale, et je sens qu’on ne restera pas longtemps le gosier sec.
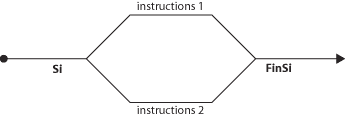
Graphiquement, on peut très facilement représenter un SI comme un aiguillage de chemin de fer
(ou un aiguillage de train électrique, c’est moins lourd à porter). Un SI
ouvre donc deux voies, correspondant à deux traitements différents. Mais il
y a des tas de situations où deux voies ne suffisent pas. Par exemple, un
programme devant donner l’état de l’eau selon sa température doit pouvoir
choisir entre trois réponses possibles (solide, liquide ou gazeuse).
Une première solution serait la suivante :
Variable Temp en Entier
Début Ecrire "Entrez la température de l’eau :" Lire Temp Si Temp =< 0 Alors Ecrire "C’est de la glace" FinSi Si Temp > 0 Et Temp < 100 Alors Ecrire "C’est du liquide" Finsi Si Temp > 100 Alors Ecrire "C’est de la vapeur" Finsi Fin
Vous constaterez que c’est un peu laborieux. Les conditions se ressemblent plus ou moins, et
surtout on oblige la machine à examiner trois tests successifs alors que
tous portent sur une même chose, la température de l'eau (la valeur de la variable Temp). Il serait ainsi bien plus rationnel d’imbriquer
les tests de cette manière :
Variable Temp en Entier
Début Ecrire "Entrez la température de l’eau :" Lire Temp Si Temp =< 0 Alors Ecrire "C’est de la glace" Sinon Si Temp < 100 Alors Ecrire "C’est du liquide" Sinon Ecrire "C’est de la vapeur" Finsi Finsi Fin
Nous avons fait des économies : au lieu de devoir taper trois conditions, dont
une composée, nous n’avons plus que deux conditions simples. Mais aussi, et
surtout, nous avons fait des économies sur le temps d’exécution de
l’ordinateur. Si la température est inférieure à zéro, celui-ci écrit
dorénavant « C’est de la glace » et passe
directement à la fin, sans être ralenti par l’examen d’autres
possibilités (qui sont forcément fausses).
Cette deuxième version n’est donc pas seulement plus simple à écrire et plus lisible, elle
est également plus performante à l’exécution.
Les structures de tests imbriqués sont donc un outil indispensable à la simplification et à
l’optimisation des algorithmes.
« J'ai l'âme ferroviaire : je regarde passer les vaches » (Léo Ferré)
Cette citation n’apporte peut-être pas grand chose à cet exposé, mais je l’aime bien, alors
c’était le moment ou jamais.
En effet, dans un programme, une structure SI peut être facilement comparée à un aiguillage de
train. La voie principale se sépare en deux, le train devant rouler ou sur
l’une, ou sur l’autre, et les deux voies se rejoignant tôt ou tard pour ne
plus en former qu’une seule, lors du FinSi. On peut schématiser cela ainsi :
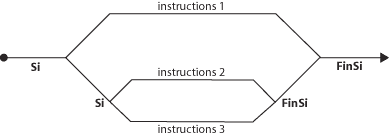
Mais dans certains cas, ce ne sont pas deux voies qu’il nous faut, mais trois, ou même
plus. Dans le cas de l’état de l’eau, il nous faut trois voies pour notre
« train », puisque l’eau peut être solide, liquide ou gazeuse. Alors, nous
n’avons pas eu le choix : pour deux voies, il nous fallait un aiguillage,
pour trois voies il nous en faut deux, imbriqués l’un dans l’autre.
Cette structure (telle que nous l’avons programmée à la page précédente) devrait être
schématisée comme suit :
Soyons bien clairs : cette structure est la seule possible du point de vue logique
(même si on peut toujours mettre le bas en haut et le haut en bas). Mais
du point de vue de l’écriture, le pseudo-code algorithmique admet une
simplification supplémentaire. Ainsi, il est possible (mais non obligatoire,
que l’algorithme initial :
Variable Temp en Entier
Début Ecrire "Entrez la température de l’eau :" Lire Temp Si Temp =< 0 Alors Ecrire "C'est de la glace" Sinon Si Temp < 100 Alors Ecrire "C’est du liquide" Sinon Ecrire "C’est de la vapeur" Finsi Finsi Fin devienne :
Variable Temp en Entier
Début Ecrire "Entrez la température de l’eau :" Lire Temp Si Temp =< 0 Alors Ecrire "C’est de la glace" SinonSi Temp < 100 Alors Ecrire "C’est du liquide" Sinon Ecrire "C’est de la vapeur" Finsi Fin
Dans le cas de tests imbriqués, le Sinon et le Si peuvent être fusionnés en un
SinonSi. On considère alors qu’il s’agit d’un seul bloc de test, conclu
par un seul FinSi
Le SinonSi permet en quelque sorte de créer (en réalité, de simuler) des aiguillages à plus de
deux branches. On peut ainsi enchaîner les SinonSi les uns derrière les
autres pour simuler un aiguillage à autant de branches que l’on souhaite.
Jusqu’ici, pour écrire nos tests, nous avons utilisé uniquement des conditions.
Mais vous vous rappelez qu’il existe un type de variables (les booléennes) susceptibles de stocker les valeurs VRAI ou FAUX.
En fait, on peut donc entrer des conditions dans ces variables, et tester ensuite la valeur de ces variables.
Reprenons l’exemple de l’eau. On pourrait le réécrire ainsi :
Variable Temp en Entier
Variables A, B en Booléen Début Ecrire "Entrez la température de l’eau :" Lire Temp A ← Temp =< 0 B ← Temp < 100 Si A Alors Ecrire "C’est de la glace" SinonSi B Alors Ecrire "C’est du liquide" Sinon Ecrire "C’est de la vapeur" Finsi Fin
A priori, cette technique ne présente guère d’intérêt : on a alourdi plutôt qu’allégé
l’algorithme de départ, en ayant recours à deux variables supplémentaires.
|