|
|
Préambule : Le Codage
« L’information n’est pas le savoir. Le
savoir n’est pas la sagesse. La sagesse n’est pas la beauté. La beauté n’est
pas l’amour. L’amour n’est pas la musique, et la musique, c’est ce qu’il y a
de mieux. » - Frank Zappa
« Les ordinateurs sont comme les dieux de
l’Ancien Testament : avec beaucoup de règles, et sans pitié. » - Joseph Campbell
« Compter en octal, c’est comme compter en
décimal, si on n’utilise pas ses pouces » - Tom Lehrer
« Il y a 10 sortes de gens au monde : ceux qui connaissent le binaire et les autres » - Anonyme
C’est bien connu, les ordinateurs sont comme le gros rock qui tâche :
ils sont binaires.
Mais ce qui est moins connu, c’est ce que ce qualificatif de « binaire »
recouvre exactement, et ce qu’il implique. Aussi, avant de nous plonger dans
les arcanes de l’algorithmique proprement dite, ferons-nous un détour par la
notion de codage binaire.
Contrairement aux apparences, nous ne sommes pas éloignés de notre sujet
principal. Tout au contraire, ce que nous allons voir à présent constitue un
ensemble de notions indispensables à l’écriture de programmes. Car pour
parler à une machine, mieux vaut connaître son vocabulaire…
De nos jours, les ordinateurs sont ces machines merveilleuses capables de
traiter du texte, d’afficher des tableaux de maître, de jouer de la musique
ou de projeter des vidéos. On n’en est pas encore tout à fait à HAL,
l’ordinateur de 2001 Odyssée de l’Espace, à « l’intelligence » si
développée qu’il a peur de mourir… pardon, d’être débranché. Mais
l’ordinateur paraît être une machine capable de tout faire.
Pourtant, les ordinateurs ont beau sembler repousser toujours plus loin les
limites de leur champ d’action, il ne faut pas oublier qu’en réalité, ces
fiers-à-bras ne sont toujours capables que d’une seule chose : faire des
calculs, et uniquement cela. Eh oui, ces gros malins d’ordinateurs sont
restés au fond ce qu’ils ont été depuis leur invention : de vulgaires
calculatrices améliorées !
Lorsqu’un ordinateur traite du texte, du son, de l’image, de la vidéo, il
traite en réalité des nombres. En fait, dire cela, c’est déjà lui faire trop
d’honneur. Car même le simple nombre « 3 » reste hors de portée de
l’intelligence d’un ordinateur, ce qui le situe largement en dessous de
l’attachant chimpanzé Bonobo, qui sait, entre autres choses, faire des
blagues à ses congénères et jouer au Pac-Man. Un ordinateur manipule
exclusivement des informations binaires,
dont on ne peut même pas dire sans être tendancieux qu’il s’agit de
nombres.
Mais qu’est-ce qu’une information binaire ? C’est une information qui ne
peut avoir que deux états : par exemple, ouvert - fermé, libre – occupé,
militaire – civil, assis – couché, blanc – noir, vrai – faux, etc. Si l’on
pense à des dispositifs physiques permettant de stocker ce genre
d’information, on pourrait citer : chargé – non chargé, haut – bas, troué –
non troué.
Je ne donne pas ces derniers exemples au hasard : ce sont précisément ceux dont
se sert un ordinateur pour stocker l’ensemble des informations qu’il va
devoir manipuler. En deux mots, la mémoire vive (la « RAM ») est formée de
millions de composants électroniques qui peuvent retenir ou relâcher une
charge électrique. La surface d’un disque dur, d’une bande ou d’une
disquette est recouverte de particules métalliques qui peuvent, grâce à un
aimant, être orientées dans un sens ou dans l’autre. Et sur un CD-ROM, on
trouve un long sillon étroit irrégulièrement percé de trous. Ainsi, un ordinateur,
c'est une machine capable de stocker et de manipuler des informations binaires. Rien de moins, mais rien de plus.
Mais tout cela concerne les concepteurs des ordinateurs ; les utilisateurs et les programmeurs, eux,
s'en fichent un peu de savoir sous quelle forme physique la machine
stocke une information donnée. Ce qui les intéresse, c'est l'information elle-même.
Alors, la coutume veut qu’on symbolise une information binaire, quel que
soit son support physique, sous la forme de 1 et de 0.
Il faut bien
comprendre que ce n’est là qu’une représentation,
une image commode, que l’on utilise pour parler de toute information
binaire. Dans la réalité physique, il n’y a pas plus de 1 et de 0 qui se
promènent dans les ordinateurs qu’il n’y a écrit, en lettres géantes,
« Océan Atlantique » sur la mer quelque part entre la Bretagne et les
Antilles. Le 1 et le 0 dont parlent les informaticiens sont des signes, ni
plus, ni moins, pour désigner une information, indépendamment de son support
physique.
Les informaticiens seraient-ils des gens tordus, possédant un goût immodéré
pour l’abstraction, ou pour les jeux intellectuels alambiqués ? Non, pas
davantage en tout cas que le reste de leurs contemporains non-informaticiens.
En fait, chacun d’entre nous pratique ce genre d’abstraction tous les jours,
sans pour autant trouver cela bizarre ou difficile. Simplement, nous le
faisons dans la vie quotidienne sans y penser. Et à force de ne pas y
penser, nous ne remarquons même plus quel mécanisme subtil d’abstraction est
nécessaire pour pratiquer ce sport.
Lorsque nous disons que 4+3=7 (ce qui reste, normalement, dans le domaine de
compétence mathématique de tous ceux qui lisent ce cours !), nous manions de
pures abstractions, représentées par de non moins purs symboles ! Un être
humain d’il y a quelques millénaires se serait demandé longtemps qu’est-ce
que c’est que « quatre » ou « trois », sans savoir quatre ou trois
« quoi ? ». Mine de rien, le fait même de concevoir des nombres,
c’est-à-dire de pouvoir considérer, dans un ensemble, la quantité
indépendamment de tout le reste, c’est déjà une abstraction très hardie, qui
a mis très longtemps avant de s’imposer à tous comme une évidence. Et le
fait de faire des additions sans devoir préciser des additions « de
quoi ? », est un pas supplémentaire qui a été encore plus difficile à
franchir.
Le concept de nombre, de quantité pure, a donc constitué un immense progrès
(que les ordinateurs n’ont quant à eux, je le répète, toujours pas
accompli). Mais si concevoir les nombres, c’est bien, posséder un système de
notation performant de ces nombres, c’est encore mieux. Et là aussi,
l’humanité a mis un certain temps (et essayé un certain nombre de pistes qui
se sont révélées être des impasses) avant de parvenir au système actuel, le
plus rationnel. Ceux qui ne sont pas convaincus des progrès réalisés en ce
domaine peuvent toujours essayer de résoudre une multiplication comme 587 x
644 en chiffres romains, on leur souhaite bon courage !
Pour comprendre comment on entre les nombres dans ce qui sert de cerveau aux ordinateurs, il faut commencer par comprendre
comment nous autres, êtres humains, représentons et manipulons les nombres. L’humanité actuelle, pour représenter n’importe quel nombre, utilise un
système de numération de position, à
base décimale. Qu’est-ce qui se cache
derrière cet obscur jargon ?
Commençons par la numération de position.
Pour représenter un nombre, aussi grand soit-il, nous disposons d’un
alphabet spécialisé : une série de 10
signes qui s’appellent les chiffres. Et lorsque nous écrivons un nombre en
mettant certains de ces chiffres les uns derrière les autres, l’ordre dans
lequel nous mettons les chiffres est capital. Ainsi, par exemple, 2569
n’est pas du tout le même nombre que 9562. Pourquoi ? Quel opération,
quel décodage mental effectuons-nous lorsque nous lisons une suite de
chiffres représentant un nombre ? Le problème, c’est que nous sommes
tellement habitués à faire ce décodage de façon instinctive que généralement
nous ne sommes même plus capables de formuler consciemment les règles que nous appliquons ! Mais ce n’est pas très compliqué de
les reconstituer… Et c’est là que nous mettons le doigt en plein dans la
deuxième caractéristique de notre système de notation numérique : son
caractère décimal.
Lorsque j’écris 9562, de quel nombre est-ce que je parle ? Décomposons la
lecture chiffre par chiffre, de gauche à droite :
9562, c’est 9000 + 500 + 60 + 2.
Allons plus loin, même si cela paraît un peu bébête :
On peut encore écrire ce même nombre d’une manière légèrement différente. Au lieu de :
9 562 = 9 x 1 000 + 5 x 100 + 6 x 10 + 2,
On écrit que :
9 562 = (9 x 10 x 10 x 10) + (5 x 10 x 10) + (6 x 10) + (2)
Arrivés à ce stade de la compétition, je prie les allergiques de m’excuser,
mais il nous faut employer un petit peu de jargon mathématique. Ce n’est pas
grand-chose, et on touche au but. Alors, courage ! En fait, ce jargon se
résume au fait que les matheux notent la ligne ci-dessus à l’aide du symbole
de « puissance ». Cela donne :
9 562 = 9 x 103 + 5 x 102 + 6 x 101 + 2 x 100
Et voilà, nous y sommes. Nous avons dégagé le mécanisme général de la
représentation par numération de position en base décimale.
Alors, nous en savons assez pour conclure sur les conséquences du choix de
la base décimale. Il y en a deux, qui n’en forment en fin de compte qu’une
seule :
Un dernier mot concernant le choix de la base dix. Pourquoi celle-là et pas
une autre ? Après tout, la base dix n’était pas le seul choix possible. Les
babyloniens, qui furent de brillants mathématiciens, avaient en leur temps
adopté la base 60 (dite sexagésimale).
Cette base 60 impliquait certes d’utiliser un assez lourd alphabet numérique
de 60 chiffres. Mais c’était somme toute un inconvénient mineur, et en
retour, elle possédait certains avantages non négligeables. 60 étant un
nombre divisible par beaucoup d’autres (c’est pour cette raison qu’il avait
été choisi), on pouvait, rien qu’en regardant le dernier chiffre, savoir si
un nombre était divisible par 2, 3, 4, 5, 6, 10, 12, 15, 20 et 30. Alors
qu’en base 10, nous ne pouvons immédiatement répondre à la même question que
pour les diviseurs 2 et 5. La base sexagésimale a certes disparu en tant que
système de notation des nombres. Mais Babylone nous a laissé en héritage sa
base sexagésimale dans la division du cercle en soixante parties (pour
compter le temps en minutes et secondes), et celle en 6 x 60 parties (pour
les degrés de la géométrie et de l’astronomie).
Alors, pourquoi avons-nous adopté la base décimale, moins pratique à bien
des égards ? Nul doute que cela tienne au dispositif matériel grâce auquel
tout être humain normalement constitué stocke spontanément une information
numérique : ses doigts !
Profitons-en pour remarquer que le professeur Shadoko avait inventé exactement
le même système, la seule différence étant qu'il avait choisi la base 4
(normal, les shadoks n'avaient que 4 mots). Regardez donc la video qui se trouve
sur cette page - ou comment
faire rigoler les gens en ne disant (presque) que des choses vraies. J'ajoute que c'est l'ensemble des videos des shadoks, et en
particulier celles traitant de la logique et des mathématiques, qui vaut son pesant
de cacahuètes interstellaires. Mais hélas cela nous éloignerait un peu trop de notre propos
(c'est pas grave, on y reviendra à la prochaine pause).
2.2 La numération de position en base binaire
Les ordinateurs, eux, comme on l’a vu, ont un dispositif physique fait pour
stocker (de multiples façons) des informations binaires. Alors, lorsqu’on
représente une information stockée par un ordinateur, le plus simple est
d’utiliser un système de représentation à deux chiffres : les fameux 0 et 1.
Mais une fois de plus, je me permets d’insister, le choix du 0 et du 1 est
une pure convention, et on aurait pu choisir n’importe quelle autre paire de
symboles à leur place.
Dans un ordinateur, le dispositif qui permet de stocker de l’information est donc
rudimentaire, bien plus rudimentaire que les mains humaines. Avec des mains
humaines, on peut coder dix choses différentes (en fait bien plus, si l’on
fait des acrobaties avec ses doigts, mais écartons ce cas). Avec un
emplacement d’information d’ordinateur, on est limité à deux choses
différentes seulement. Avec une telle information binaire, on ne va pas
loin. Voilà pourquoi, dès leur invention, les ordinateurs ont été conçus
pour manier ces informations par paquets de 0 et de 1. Et la taille de ces
paquets a été fixée à 8 informations binaires.
Une information binaire (symbolisée couramment par 0 ou 1) s’appelle un bit
(en anglais... bit).
Un groupe de huit bits s’appelle un octet (en anglais, byte) Donc, méfiance avec le byte (en abrégé, B majuscule), qui vaut un octet, c'est-à-dire huit bits (en abrégé, b minuscule).
Dans combien d’états différents un octet peut-il se trouver ? Le calcul est assez facile (mais il faut
néanmoins savoir le refaire). Chaque bit de l’octet peut occuper deux états.
Il y a donc dans un octet :
2 x 2 x 2 x 2 x 2
x 2 x 2 x 2 = 28 = 256 possibilités
Cela signifie qu’un octet peut servir à coder 256 nombres différents : ce
peut être la série des nombres entiers de 1 à 256, ou de 0 à 255, ou de –127
à +128. C’est une pure affaire de convention, de choix de codage. Mais ce
qui n’est pas affaire de choix, c’est le nombre de possibilités : elles sont
256, pas une de plus, pas une de moins, à cause de ce qu’est, par
définition, un octet.
Si l’on veut coder des nombres plus grands que 256, on va donc être contraint de mobiliser plus d’un
octet. Et c'est ce qu'on fait aussi pour coder des nombres négatifs, ou décimaux. Ce n’est pas un problème, et c’est très souvent que les ordinateurs
procèdent ainsi.
En effet, avec deux octets, on a 256 x 256 = 65 536 possibilités.
En utilisant trois octets, on passe à 256 x 256 x 256 = 16 777 216
possibilités.
Je ne vais aborder ici que le codage des nombres le plus simple : celui qui code les nombres entiers à partir de zéro.
Je me limiterai au cas à on ne dispose que d'un octet, mais en fait, le principe est exactement le même si on dispose de deux, trois ou quatre octets.
Je rappelle qu’un octet peut coder 256 nombres différents, donc, en l'occurrence, la série des entiers de 0 à 255.
Comment faire pour, à partir d’un
octet, reconstituer le nombre dans la base décimale qui nous est plus
familière ? Ce n’est pas sorcier ; il suffit d’appliquer, si on les a bien
compris, les principes de la numération de position, en gardant à l’esprit
que là, la base n’est pas décimale, mais binaire. Prenons un octet au
hasard :
1 1 0 1 0 0 1 1
D'après les principes vus plus haut, ce nombre représente (lisons-le de gauche à droite) :
1 x 27 + 1 x 26 + 0 x 25 + 1 x 24 + 0 x 23
+ 0 x 22 + 1 x 21 + 1 x 20 =
1 x 128 + 1 x 64 + 1 x 16 + 1 x 2 + 1 x 1 =
128 + 64 + 16 + 2 + 1 =
211
Et voilà ! Ce n’est pas plus compliqué que cela !
Inversement, comment traduire un nombre décimal en codage binaire ? Il
suffit de rechercher dans notre nombre les puissances successives de deux. C'est un peu plus pénible, et il faut impérativement
commencer par les chiffres de gauche, c'est-à-dire par les plus grandes puissances de 2. C'est parti : prenons, par exemple, 186.
Dans 186, on trouve 1 x 128, soit 1 x 27. Je retranche 128 de 186 et j’obtiens 58.
Dans 58, on trouve 0 x 64, soit 0 x 26. Je ne retranche donc rien.
Dans 58, on trouve 1 x 32, soit 1 x 25. Je retranche 32 de 58 et j’obtiens 26.
Dans 26, on trouve 1 x 16, soit 1 x 24. Je retranche 16 de 26 et j’obtiens 10.
Dans 10, on trouve 1 x 8, soit 1 x 23. Je retranche 8 de 10 et j’obtiens 2.
Dans 2, on trouve 0 x 4, soit 0 x 22. Je ne retranche donc rien.
Dans 2, on trouve 1 x 2, soit 1 x 21. Je retranche 2 de 2 et j’obtiens 0.
Dans 0, on trouve 0 x 1, soit 0 x 20. Je ne retranche donc rien.
Il ne me reste plus qu’à reporter ces différents résultats (dans l’ordre !)
pour reconstituer l’octet. J’écris alors qu’en binaire, 186 est représenté
par :
1 0 1 1 1 0 1 0
C’est bon ? Alors on passe à la suite.
2.3 Le codage hexadécimal
Nos aventures avec les nombres ne sont pas terminées. Nous avons en effet d'un côté les nombres décimaux, qu'utilisent les humains,
mais qui n'ont rien à voir avec le codage utilisé par les machines. Celles-ci fonctionnent avec des nombres écrits en binaire... qui sont
une catastrophe pour l'humanité (si vous ne me croyez pas, essayez donc de dicter un long nombre binaire à quelqu'un, je ne vous donne pas
30 secondes pour devenir chèvre).
Aussi, on a remarqué qu'il existait une base qui pouvait servir d'intermédiaire aux humains et aux machines.
C'est une base qui se trouve en quelque sorte à mi-chemin entre la base décimale et la base binaire :
la base seize, qui produit donc le codage hexadécimal.
Pourquoi ce choix bizarre ? Parce qu'une suite de huits bits peut très facilement être considérée comme deux
groupes de 4 bits (les quatre de gauche, et les quatre de droite). 4 bits, cela permet de coder
2 x 2 x 2 x 2 = 16 nombres différents. Donc, un octet, au lieu d'être considéré comme un nombre binaire de huit chiffres,
peut être considéré comme un nombre hexadécimal de deux chiffres. Et deux chiffres, c'est quatre fois plus pratique que huit !
Comme en codage hexadécimal, on utilise une série de seize chiffres (logique !), se pose le problème de choisir les signes qui vont représenter
ces seize chiffres. Pour les dix premiers, on n’a pas
été chercher bien loin : on a recyclé les dix chiffres de la base décimale.
Les dix premiers chiffres de la base seize sont donc tout bêtement 0,
1, 2, 3, 4, 5, 6, 7, 8, et 9. Mais là, il manquait encore 6 chiffres, pour
représenter les nombres que nous écrivons en décimal 10, 11, 12, 13, 14 et 15.
Plutôt qu’inventer de nouveaux symboles (ce qu’on aurait très bien pu
faire), on a choisi de recycler les premières lettres de l’alphabet. Ainsi, par
convention, A vaut 10, B vaut 11, etc. jusqu’à F qui vaut 15.
Comme on le disait, la base hexadécimale permet une représentation très
simple des octets du binaire. Prenons un octet au hasard :
1 0 0 1 1 1 1 0
Pour convertir ce nombre en hexadécimal, il y a deux méthodes : l’une
consiste à faire un grand détour, en repassant par la base décimale. C’est
un peu plus long, mais on y arrive. L’autre méthode consiste à faire le
voyage direct du binaire vers l’hexadécimal. Avec l’habitude, c’est
nettement plus rapide !
Première méthode :
On retombe sur un raisonnement déjà abordé. Cet octet représente en base dix :
1 x 27 + 0 x 26 + 0 x 25 + 1 x 24 + 1 x 23
+ 1 x 22 + 1 x 21 + 0 x 20 =
1 x 128 + 1 x 16 + 1 x 8 + 1 x 4 + 1 x 2 + 0 x 1 =
128 + 16 + 8 + 4 + 2 =
158
De là, il faut repartir vers la base hexadécimale.
Dans 158, on trouve 9 x 16, c’est-à-dire 9 x 161. Je retranche 144 de 158 et j’obtiens 14.
Dans 14, on trouve 14 x 1, c’est-à-dire 14 x 160. On y est.
Le nombre s’écrit donc en hexadécimal : 9E
Deuxième méthode :
Divisons 1 0 0 1 1 1 1 0 en 1 0 0 1 (partie gauche) et 1 1 1 0 (partie droite).
1 0 0 1, c’est 8 + 1, donc 9
1 1 1 0, c’est 8 + 4 + 2 donc 14
Le nombre s’écrit donc en hexadécimal : 9E. C’est la même conclusion qu’avec la première
méthode. Encore heureux !
Le codage hexadécimal est très souvent utilisé quand on a besoin de
représenter les octets individuellement, car dans ce codage, tout octet
correspond à seulement deux signes. En hexadécimal, le nombre le plus petit que puisse contenir un octet s'écrit évidemment 00.
Et le nombre le plus grand (correspondant à 255 en décimal) s'écrit FF.
Si les ordinateurs n'étaient capables que de traiter des nombres, ils n'auraient pas eu le succès que l'on sait. Or, nous savons tous que les ordinateurs savent faire des tas d'autres choses, à commencer par manipuler des textes : c'est le cas lorsqu'on utilise un traitement de texte, lorsqu'on envoie un email, lorsqu'on affiche une page web, etc. Mais comme on l'a déjçà dit, en réalité, les ordinateurs ne manipulent pas vraiment des textes : ils manipulent des informations binaires, qui codent du texte. On va donc maintenant voir de quelle façon.
La première chose à dire, c'est que lorsqu'on parle de coder du texte, on met de côté les mises en forme de ce texte : choix de la police, taille des marges, gras, italique, etc. Pour tout cela, les traitements de texte mobilisent des octets supplémentaires, qui stockent ces informations. Mais ici, je ne parle que du texte lui-même : celui qui apparaît sans aucune mise en forme dans le « bloc-notes » de l'ordinateur, par exemple, et qu'on appelle le texte brut.
L'informatique est apparue aux États-Unis après la deuxième guerre mondiale, et la première langue qu'il fallait coder était l'anglais. Or, l'anglais s'écrit avec l'alphabet latin : il utilise donc 26 lettres (majuscules et minuscules), 10 chiffres, et quelques dizaines de signes de ponctuation. Au total, écrire l'anglais nécessite donc une centaine de caractères. Les ordinateurs étant construits à partir de paquets de 8 bits (les octets), et chaque octect étant capable de stocker 256 possibilités, le choix était vite fait : on pouvait coder le texte sur le principe 1 caractère = 1 octet. Les valeurs d'octet qui ne correspondaient à aucun signe d'écriture pouvaient même être utilisées pour représenter divers petits signes graphiques (des flèches, des mini-smileys, et des symboles variés).
Le problème, c'est que s'il existe une logique simple qui permet de coder les nombres en binaire, cette logique fait défaut en ce qui concerne les textes : la correspondance entre telle valeur d'octet et tel signe alphanumérique est parfaitement arbitraire. Du coup, dans les débuts de l'informatique, chaque concepteur d'ordinateur ou de logiciel avait créé sa propre table de correspondance. Mais du coup, les échanges de textes entre logiciels, ou entre machines, tournaient au casse-tête : le T majuscule de l'un devenait une parenthèse ouvrante chez l'autre !
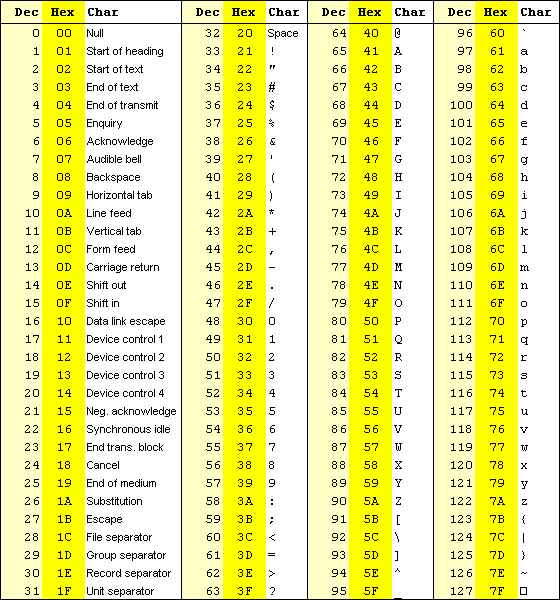
C'est pourquoi dès le début des années 1960, une autorité édicta un standard, une table de correspondance à laquelle tous devaient se plier ; cette table de correspondance, qui utilisait uniquement 128 premières valeurs de l'octet (celes dont le premier bit est un zéro) les est connue sous le nom de code ASCII (pour American Standard Code for Information Interchange). Dès lors, le A majuscule, par exemple, était codé par la valeur d'octet 01000001 (65, en notation décimale) quelle que soit la machine et le logiciel utilisés, et les textes pouvaient être transmis d'une machine à l'autre sans se changer en un charabia incompréhensible.
Dans un deuxième temps, l'informatique s'est étendue, essentiellement vers l'Europe. Et là, nouveau problème : les Européens de l'ouest (surtout les Français !) utilisent, en plus des caractères standard de l'alphabet latin, toute une série de caractères particuliers (accents, o barrés, jota...). Ces caractères étaient trop nombreux pour qu'on puisse les faire tous loger dans la table ASCII à 256 possibilités. On a donc adopté la solution suivante : les 128 premières positions de la table conservaient les caractères latins communs à toutes les langues (ceux de la table ASCII de base). Ensuite, pour chaque langue, ou groupe de langues, on a créé un codage spécifique des 128 dernières positions (dont le premier bit vaut 1). C'est là que se concentrent tous les caractères accentués du français, par exemple. Il y a donc une « page » de codes propre à chaque ensemble de langue latine. C'est la raison pour laquelle il arrive (en fait, il arrivait, car c'est de moins en moins fréquent) qu'on récupère un texte dont tous les caractères accentués (mais seulement eux) étaient illisibles. Cela voulait simplement dire qu'au cours des pérégrinations du texte, une mauvaise version nationale de page avait été employée ; la deuxième partie de la table ASCII avait donc été mal encodée ou décodée...
Aussi longtemps que l'informatique a concerné des langues alphabétiques, fussent-elles non latines, tout allait bien : il suffisait d'employer une autre table de codage nationale, toujours sur le même principe 1 caractère = 1 octet. Les vrais soucis sont arrivés lorsqu'il a fallu coder des langues non alphabétiques, comme le chinois. L'écriture chinoise utilise en effet des milliers d'idéogrammes différents. Impossible de coder des milliers de possibilités avec un seul octet... Voilà pourquoi, depuis plusieurs années, un nouveau système de codage a vu le jour : l'Unicode, pour « codage universel ». L'idée, toute simple, consistait au départ à réserver désormais deux octets au lieu d'un seul pour coder chaque caractère. Avec deux octets, on peut coder 256 x 256 = 65 536 possibilités (soit 2 puissance 16, je vous laisse vérifier !). C'est largement assez pour coder n'importe quelle écriture du monde, même la plus dispendieuse en caractères. En réalité, c'est bien plus compliqué que cela, et les curieux pourront se plonger dans les arcanes du code international des caractères en consultant, par exemple, "la longue page Wikipedia consacrée à ce sujet.
Pour terminer sur ce point, un rapide calcul : les différents livres et articles que j'ai pu écrire sur des sujets passionnants et assez éloignés de l'informatique (la naissance des inégalités, l'origine de la domination masculine, la nature du profit, j'en passe et des plus stimulants) doivent, à eux tous, représenter à peu près 1000 pages de texte. Sachant que sur une page de livre normal, on fait entrer environ 2500 caractères, cela veut dire qu'en plusieurs années de recherche, j'ai produit environ 2 500 000 caractères. Une fois codés en texte brut, ces recherches représentent donc 2 500 000 octets (2,5 Mo) dans le codage traditionnel, 5 000 000 octets (5 Mo) dans le codage Unicode. Gardons ces chiffres en tête, on y reviendra...
Nous le savons tous : les ordinateurs sont depuis longtemps capable d'enregistrer et de jouer de la musique. Et indépendamment même des ordinateurs, le son est devenu « digital ». Qu'est-ce que cela signifie ? Que le son est désormais, lui aussi, codé sous forme d'une suite d'informations binaires. Mais pour comprendre comment, il faut comprendre ce qu'est un son, et comment il était enregistré et restitué dans les appareils traditionnels.
Le son est la vibration d'un milieu (disons, pour faire simple, l'air). Ce que nous appelons un son, c'est l'oscillation de la pression de l'air. Toute oscillation n'est pas perceptible par nos oreilles ; pour que ce soit le cas, il faut qu'il y ait au minimum 20 vibrations par secondes (20 Hertz) et au maximum 20 000. Au-delà, le son existe, mais nous ne le percevons pas... contrairement à nos amimaux de comagnie préférés. Voilà pourquoi, quand on souffle dans un sifllet à ultra-sons, on a l'impression de ne produire que du vent, tandis que le toutou et le minet de la maison filent ventre à terre, les tympans déchirés...
Traditionnellement, on s'efforçait d'enregistrer le son en employant des dipositifs qui collaient au plus près au phénomène physique initial, à savoir les variations de la pression de l'air : on transformait ces variations en variations équivalentes de courant électrique avec un micro (au passage, nos oreilles font exactement la même chose), puis ce courant électrique était lui même transformé en ocillations du sillon sur un disque de cire, ou de particules métalliques sur une bande magnétique. Pour la restitution du son, on avait un dispositif qui effectuait exactement la même série de transformations, mais dans l'autre sens. En bout de chaîne, par exemple, les enceintes d'une chaîne hi-fi ne sont rien d'autre que des micros inversés, qui transforment une oscillation de courant électrique en oscillations de l'air. Tout le principe, dans un sens comme dans l'autre, était de parvenir à chaque fois, à changer la forme physique du signal en le déformant le moins possible : on procédait donc par analogie, et on parle à ce propos de son « analogique ».
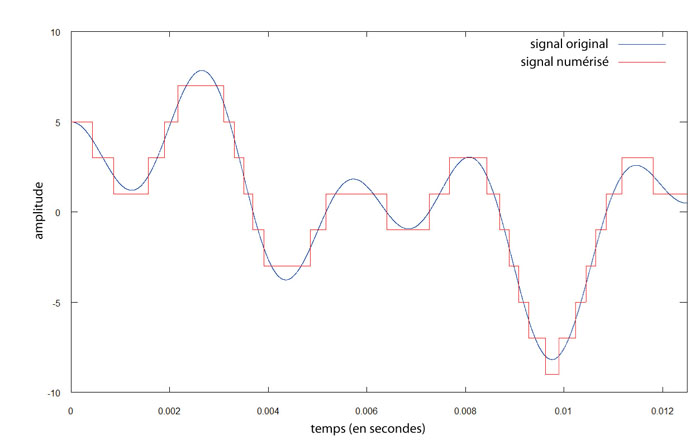
Lorsqu'on passe au son « numérique », tout change. Avec des informations binaires, quoi qu'on fasse, il est strictement impossible de restituer quelque chose de continu (une courbe, une oscillation). Impossible donc de procéder par analogie : la seule chose qu'on puisse faire, c'est prendre des mesures à intervalles réguliers. C'est un peu comme au cinéma : on n'enregistre pas vraiment le mouvement, mais on enregistre suffisamment d'images fixes pour que l'illusion soit parfaite et que nos yeux perçoivent du mouvement là où il n'y en a pas vraiment. Le son numérique ne code donc pas une courbe - il en est incapable - mais, en quelque sorte, des marches d'escalier qui sont suffisamment petites et rapprochées pour donner l'illusion d'une courbe...
Lorsque le format CD a été imaginé, il fallait trouver un compromis. D'un côté, plus les mesures seraient nombreuses et précises, plus les marches d'escalier seraient petites et proches de la courbe initiale, et plus la restitution serait fidèle. De l'autre côté, la précision est coûteuse en octets, en capacité de stockage et en puissance de traitement. Il fallait donc choisir la précision acceptable, mais pas davantage. En ce qui concerne le nombre de mesures par seconde, les physiciens ont établi que pour s'approcher convenablement d'une courbe qui peut varier 20 000 fois par seconde, il faut prendre environ le double de mesures. Le standard pour le CD a donc été fixé à 44 100 mesures par seconde. Quand à leur précision, il a été décidé d'utiliser 16 bits (2 octets) par mesure, soit 65 536 niveaux possibles d'intensité. Avec un tel standard, l'oreille humaine n'est virtuellement pas capable d'entendre la dégradation du signal par rapport à la courbe d'origine : le son numérique produit alors un résultat (presque) parfait, et peut rivaliser avec le son analogique.
Essayons d'estimer rapidement la quantité d'information requise pour du son au format CD. Une seconde de son nécessite 44 100 mesures occupant chacune 2 octets. Comme il ne faut pas oublier que le format CD est en stéréo, chaque seconde est en réalité enregistrée deux fois, une pour la voie de gauche, une pour la droite. Cela veut dire qu'une seconde de son CD requiert 44 100 x 2 x 2 = 180 000 octets environ. Une minute requiert 60 fois plus, soit à peu près 10 000 000 octets (10 Mo). C'est cohérent : sur un CD, il y a 700 Mo disponibles. Or, la durée maximale d'un CD audio est de 74 mn. Cela prouve que nos calculs, à des détails près, sont justes.
Et, pour conclure cette partie, on en arrive à une pensée vertigineuse. Rappelez-vous que plusieurs années de recherches assidues ont abouti, dans mon cas personnel, à produire environ 2,5 Mo de connaissances sous forme de texte brut - le double si l'on code généreusement en Unicode. Eh bien, quoi qu'il en soit, la conclusion s'impose, dure mais imparable : il y a beaucoup plus d'informations dans une minute de n'importe quel morceau de David Guetta que dans toutes mes publications réunies.
Voilà une vérité qui, lorsqu'on en prend conscience, invite à une grande modestie.
Pour les images (puis les vidéos), le problème était un peu le même que pour le son. Une image, normalement, est un phénomène continu, que ce soit au niveau des formes (il y a des courbes), ou au niveau des couleurs (il y a des transitions imperceptibles et une infinité de nuances). Or, quitte à me répéter, les ordinateurs sont incapables de gérer quoi que ce soit de continu - mais ils peuvent faire semblant...
Le principe de la numérisation de l'image ressemble donc à celui du son : on va découper l'image en petits carrés appelés pixels, et on va assigner à chacun de ces carrés une couleur parmi un nombre limité. Le truc, c'est que plus les carrés seront denses, et donc petits, et plus le nombre de couleurs sera élevé, plus l'oeil humain finira par voir des courbes là où il n'y a que des marches d'escalier, et des dégradés de couleurs là où il n'y a qu'une juxtaposition. Si le découpage est trop grossier, ou les couleurs trop peu nombreuses, comme c'était le cas dans les débuts de l'informatique, l'image était manifestement dégradée, et on parle dans ce cas de pixellisation.
Le nombre de pixels définit ce qu'on appelle la résolution, et on peut mesurer les progrès des performances techniques à son augmentation continue, sur les écrans d'ordinateurs ou sur les capteurs d'appareils photographiques numériques. Aujourd'hui, il est courant qu'un écran de PC affiche une résolution de 1600 x 1200 pixels : autrement dit, qu'une image occupant tout l'écran mobilise près de 2 millions de pixels. Les appareils photographiques numériques, eux, possèdent des résolutions qui sont courrament de l'ordre de 12, 16 voire 20 ou 24 millions de pixels. Naturellement, cela signifie que le poids en octets d'une image est d'autant plus élevé, puisqu'il faut ensuite coder la couleur pour chaque pixel de l'image.
En ce qui concerne les couleurs, donc, le principe même de la numérisation est que le nombre de couleurs diponibles n'est pas infini. Sur les premiers écrans des années 1980, en mode d'affichage dit CGA, on disposait de 4 couleurs - chaqu pixel était donc codé sur 2 bits. Avec la norme VGA, au début des années 1990, on était passé à 256 couleurs, c'est-à-dire au codage de chaque pixel sur un octet complet. À l'époque tout le monde trouvait le résultat magnifique... Mais on était encore très loin de la qualité nécessaire pour bluffer l'oeil humain ! Depuis une quinzaine d'années, on est passé à un système où les couleurs sont produites par un mélange de trois couleurs primaires : le rouge, le vert et le bleu. On parle donc de couleurs RVB (RGB en anglais). Pour chacune des couleurs primaires, on dispose de 256 degrés d'intensité possibles, depuis 0 (pas du tout) jusqu'à 255 (à fond !). Chaque couleur numérique est donc le mélange de 256 nuances de rouge, 256 nuances de verte et 256 nuances de bleu. Il n'y a donc pas une infinité de couleurs disposibles, mais... un grand nombre (256 x 256 x 256, soit un peu plus de 16 millions), suffisant pour tromper nos sens et faire en sorte que l'oeil ne perçoive plus les transitions, et soit persuadé de voir des dégradés. Il va de soi que le nombre de 256 n'a pas été choisi au hasard : c'est pile poil le nombre de combinaisons possibles avec un octet, et toute cette affaire correspond simplement au fait qu'on a choisi de coder chaque pixel sur trois octets (un pour le rouge, un pour le vert, un pour le bleu) - on parle aussi de couleurs « 24 bits ».
Je terminerai sur la manière dont les couleurs sont dorénavant spécifiées en informatique, par exemple dans des logiciels graphiques tels que Photoshop, ou en HTML/CSS, pour les sites web. Toute couleur étant une combinaison des trois octets de couleurs primaires, spécifier la valeur de ces trois octets revient à spoécifier la couleur. Ainsi, si nous parlons en décimal, le noir correspond à 0 - 0 - 0, le blanc à 255 - 255 - 255, le rouge pétoire à 255 - 0 - 0, etc. Oui mais voilà, les ordinateurs parlent très mal le décimal... mais comprennent très bien l'hexadécimal. Et donc, les valeurs des octets seront spécifiées par deux chiffres hexadécimaux (je le rappelle, entre 0 et F). Cela signifie que le noir est 00 - 00 - 00, en abrégé : 000000. Que le blanc est FF - FF - FF, en abrégé, FFFFFF. Que le rouge pétoire est FF - 00 - 00, soit FF0000. Et voilà comment les dénominations des couleurs, qui semblent à première vue une sorte de formule cabalistique de magie noire, s'éclairent d'un seul coup comme une notation extrêmement logique et, finalement, assez simple...
Allez, assez bavardé, on passe aux choses sérieuses : les arcanes de l’algorithmique…
|